Motivation
Until 2000, the performance improvement of processor was mainly obtained with clock frequency improvement together with instructions per clock with the Pentium 4 being the last of its kind in the frequency race. However since then, Moore’s law has applied and translated into vector units and multi-cores.
Processor Performance
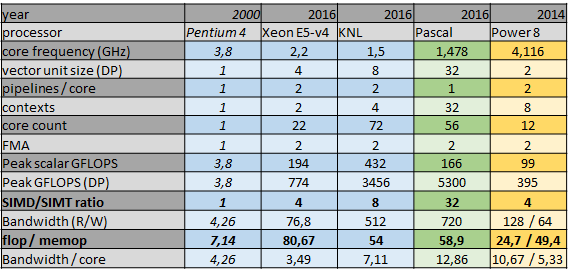
The following table illustrates a few processors performance metrics:
In most cases, frequency drops, core count and vector units explode. Also, a flop/memop metric, which is the number of arithmetic instructions that can be performed within the same time of a memory operation, increases drastically. This means that most problems get memory bound if no specific care is taken.
Note that multi-threading is not the only issue: the platform flops are only relevant if vector unit is used, and this trend gets stronger with AVX-512.
Some Experiments on Simple Operations
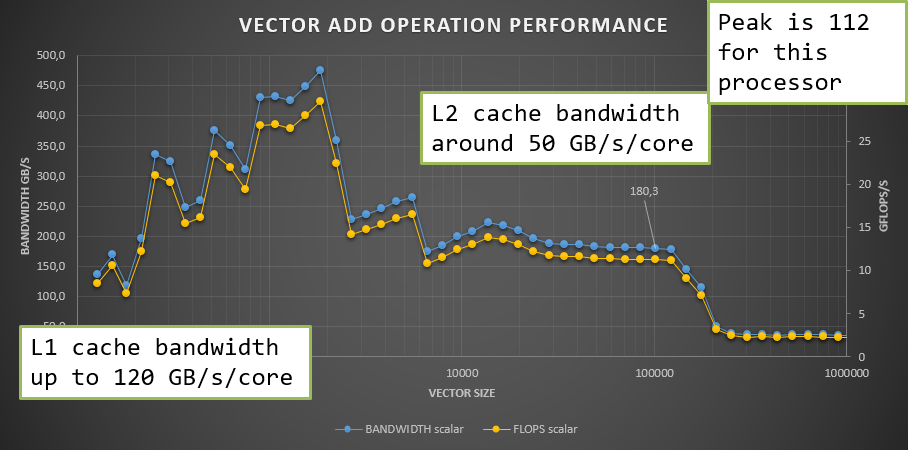
To illustrate the theoretical observations, we tried performing addition of a constant to a vector of values.
For a vector size below 2 thousand entries, that is 16kB, the whole data fits in L1 cache, and performance is very high. Even though, the arithmetic performance is barely reaching quarter of the peak. For larger sets, when fitting in the L2 cache, performance stalls at 50GB/s/core, after what the performance drops.
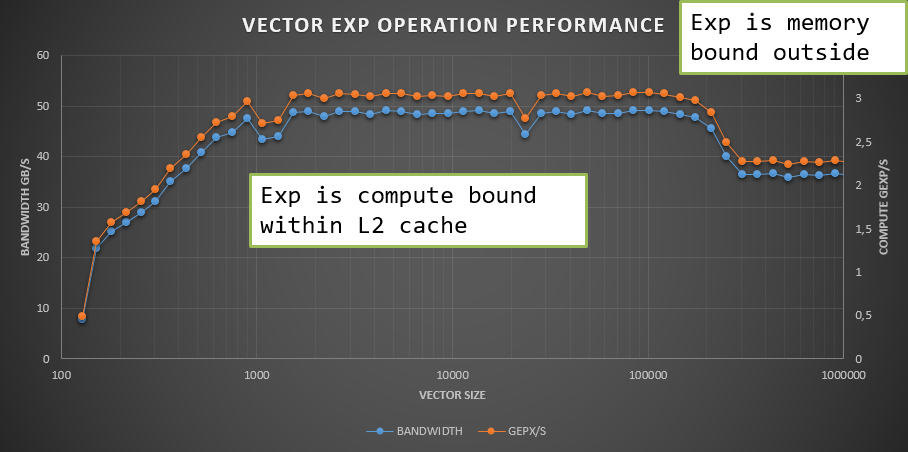
When doing the same experiment calculating the exponential of a vector of values, the performance is the same whether data is in L1 cache or L2 cache, but exp is memory bound when outside of cache.
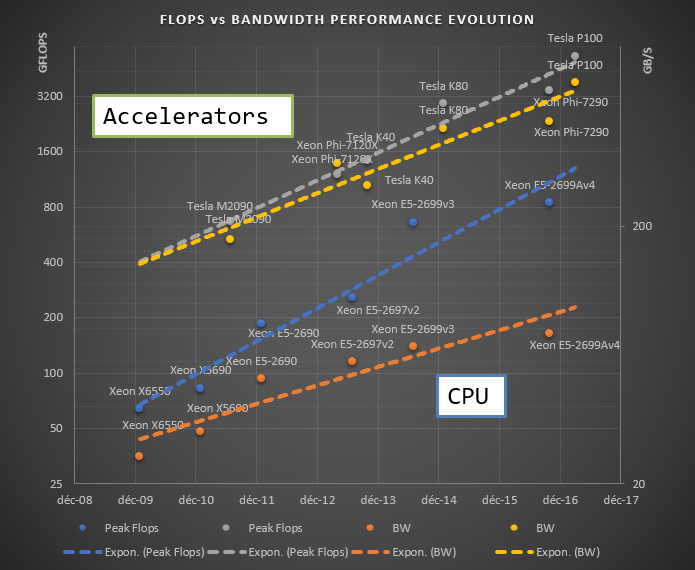
Finally, looking into bandwidth and compute evolution of processors, these two metrics do not live on the same performance improvement trend.
Decorrelate Compute from Data
The core idea of Hybrid Vector Library (HVL) is to decorrelate the expression of computations in the algorithm from the data access. The algorithm is expressed in a way independent from the data access.
This allows, without code rewrite, and possibly at runtime, change in the data access pattern, and selection of the appropriate parallel construct for optimal execution.
Discounting Cash Flows with HVL C/C++ API
The discounting of cash flows, which is a fundamental brick of quantitative finance, is expressed as follows:
Where \(T\) is maturity of the cash flow, \(c\) its notional and \(r\) the interest rate.
When running a Monte-Carlo simulation on the rate, the value of \(r\) would be different for each simulation, other parameters remaining constant.
Using the plain C API
The code to evaluate the moments for the MonteCarlo simulation is the following:
double func(int nsimul, double T, double c)
{
hybridvector* hv ;
hvl_create(&hv, nsimul); // allocate "vector"
generate_rates(hv, nsimul); // hv [i] <- r [i]
hvl_mul_scalar(hv, -T); // hv [i] <- hv [i] * (-T)
hvl_apply_exp(hv); // hv [i] <- exp (hv [i])
hvl_mul_scalar(hv, c); // hv [i] <- c * hv [i]
frozenvector* fv;
double PV;
hvl_freeze(&fv, hv); // compute moments
hvl_frozen_avg(fv, &PV); // PV <- Sum (hv [i])
hvl_destroy(hv); // clean-up
hvl_frozen_destroy(fv);
return PV;
}
In this expression, there is no explicit memory allocation, the focus is only on the algorithm: indeed, no need to repeat the same index for each table that would be used. And most importantly, the execution scheme is not provided in the algorithm: its implementation can easily differ from one implementation to another.
Using C++ Lambda Expressions
Without any loss of capability, it is also possible to express the algorithm as a lambda expression, capturing the two constants:
double func(int nsimul, double T, double c)
{
hybridvector* hv ;
hvl_create(&hv, nsimul);
generate_rates(hv, nsimul);
hvl_apply_func <>(hv, [c,T](size_t k, double rate) -> double
{
return c * ::exp(-T * rate);
});
frozenvector* fv;
double PV;
hvl_freeze(&fv, hv);<br />
hvl_frozen_avg(fv, &PV);
hvl_destroy(hv);
hvl_frozen_destroy(fv);
return PV;
}
C-Sharp
The API has been exposed in CSharp with two approaches: a plain P/Invoke wrapper where algorithm code looks very much like C code:
hybridvector hva, hvb; Hvl.hvl_create(out hva, count); Hvl.hvl_create(out hvb, count); Hvl.hvl_assign(hva, a); Hvl.hvl_assign(hvb, b); Hvl.hvl_apply_exp(hvb); Hvl.hvl_mul(hva, hvb); Hvl.hvl_assign(hvb, c); Hvl.hvl_apply_exp(hvb); Hvl.hvl_mul(hva, hvb); frozenvector res; Hvl.hvl_freeze(out res, hva, 1); Hvl.hvl_frozen_destroy(res); Hvl.hvl_destroy(hva); Hvl.hvl_destroy(hvb);
Or using a node-based approach:
IHvlResult hvlres;
HvlNode n = HvlNode.load(a) *
HvlNode.exp(HvlNode.load(b)) *
HvlNode.exp(HvlNode.load(c));
var hvlEval = HvlRuntime.CreateEvaluator(n, count);
timer.Start();
hvlres = hvlEval.Evaluate();
timer.Stop();
Implementations and Target Architectures
HVL is implemented using a variety of approaches with different applicability. The MKL implementation for instance simply maps function calls on equivalent MKL library calls where more advanced GPU implementations generate a kernel from the sequence of function calls and execute it at runtime.
A GPU implementation has been presented at GTC 2017.

Finally, the implementation can be selected at runtime allowing for optimized execution performance on an hybrid deployment environment.